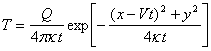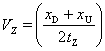Tranzflo NZ Ltd

Specialists in Sap Flow Sensors

Heat pulse theory—idealized

Tranzflo NZ Ltd,  15 Parata St, Palmerston North 4410, NEW ZEALAND

Tel:  +64-6-357-4600    Fax:     +64-6-357-4601                                                 E-mail: stevegreen@inspire.co.nz

 

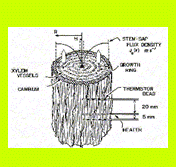
Heat-pulse methods date back some 70 years to the work of Huber (1932) who first conceived the idea of using heat as a tracer of sap flow. Some fifty years later Marshall (1958) developed a theoretical framework for heat-pulse, based on a set of analytical solutions to the following heat flow equation,

                                       Eq. [1]

that ideally represents the two dimensional pattern of temperature surrounding a line heater of zero dimension that is inserted into a section of sapwood of uniform physical and thermal properties. Here, T is the temperature departure from ambient [K], t is time [s], λ is the thermal conductivity [W m^-1 K^-1] in the axial (x) and tangential (y) directions, a is the fraction of xylem cross-sectional area occupied by sap streams moving with a velocity u in the x-direction, and Q is the amount of internal heat that is released from the heater [W m^-3].

 

Back to top

There is a simple relationship between the heat-pulse velocity, V [m s^-1], and the sap flux density, J_S = au [m s^-1], that is given by

                                                                      Eq. [2]

where ρ is the density [kg m^-3], c is the specific heat capacity [J s^-1 m^-1 K^-1] and the subscripts s and w refer to the sap and the fresh wood, respectively. Following the application of a heat-pulse, the temperature rise, T, at a distance of from the line heater is given by (Marshall, 1958)

                                                     Eq. [3]

where is the thermal diffusivity [m² s^-1] of the sapwood.

Back to top

Swanson (1962) was one of the first to utilize Marshall’s analytical solutions, in his analysis of the ‘compensation’ heat-pulse method where two temperature sensors are placed asymmetrically either side of a line heat source. Swanson showed that if the temperature rise is measured at distances x_U [m] upstream and x_D [m] downstream from the heater, then the heat-pulse velocity can be calculated from

                                                             Eq. [4]

where t_Z [s] is the time delay for the temperatures at points x_D and x_U to become equal. Equation [4] implies that the centre of the heat-pulse is convected downstream from the heater to reach a point mid-way between the two temperature sensors after a time t_Z.

Back to top

Marshall’s (1958) analytical theory was also used by Cohen et al. (1981) to develop an alternative ‘improved heat-pulse method’ that relies on measuring the time, t_M, for a maximum temperature rise to be recorded by a single sensor located a distance x_D downstream from a line heater. We shall refer to this as the ‘T-max’ method. The heat-pulse velocity, V_M [m s^-1] is calculated from

                                                Eq. [5]

The only other factor required to determine V_M is the thermal diffusivity, κ, which is determined from the following equation

                                                                 Eq. [6]

that is calculated at times when zero sap-flow occurs. The condition V_M = J_S = 0 normally occurs at night, when vapour pressure deficits are low, leaf stomata have closed and transpiration losses are close to zero. We refer to the estimate of V [m s^-1] from Eqs 4 and 5 as the ‘raw’ heat-pulse velocity.

Back to top

 

 

 

 

To contact us: